Entanglement e codice sorgente dello spazio tempo (parte quarta).
Abbiamo concluso il precedente post suggerendo l’idea che lo spazio non sia fondamentale ma emerga dalla teoria quantistica: la sfuggente “gravità quantistica” potrebbe risolversi in una meccanica quantistica da cui emerge la gravità.
Hawking nel 2004 ha riconosciuto che il calcolo relativo alla radiazione che porta il suo nome, e che prevedeva la perdita dell’informazione quantistica relativa a tutto quanto attraversi l’orizzonte degli eventi, era da qualche parte sbagliato: ma dove?
Bisognerà aspettare ancora un decennio per iniziare a capirlo.
Nel frattempo alla Relatività Generale ed alla teoria quantistica abbiamo visto essersi aggiunto un nuovo formidabile strumento che inizia a produrre risultati: la teoria olografica, che è emersa dalla corrispondenza Ads / CFT, una dualità scoperta da Juan Maldacena negli ultimissimi anni del secolo scorso facendo uso della matematica utilizzata nell'ambito della teoria delle stringhe (19).
Si applica ad un tipo di universo diverso dal nostro, dotato di 5 dimensioni e caratterizzato da una curvatura AntiDeSitter (un tipo speciale di spazio tempo della Relatività Generale con una curvatura iperbolica).
La Teoria di Campo Conforme (CFT) è invece un tipo di teoria quantistica ben nota dove la gravità - che Einstein ci insegna emergere dalla curvatura dello spazio - è assente, e sua caratteristica è la presenza di una dimensione in meno.
La CFT - quadridimensionale - codifica tutto ciò che riguarda lo spazio AdS a 5 dimensioni cui è associata: l'intera regione dello spazio tempo risulta cioè composta dalle interazioni tra gli elementi del sistema quantistico nella CFT.
Ma cosa genera la dimensione in più?
Nel 2006, sempre nell'ambito della teoria olografica, Shinsei Ryu e Tadashi Takayanagi pubblicano un articolo all'interno del quale verrà formulata una congettura divenuta in seguito nota con le lettere iniziali dei cognomi dei due fisici: la “congettura RT”.
Tale congettura, procedendo dalla corrispondenza Ads / CFT, permette di calcolare la connessione tra “entanglement quantistico” e “geometria dello spazio tempo” (20).
L’entanglement quantistico è quella “spooky action” che aveva turbato Einstein: una connessione a lunga distanza tra oggetti, che correla istantaneamente il loro comportamento “in modi statisticamente improbabili”.
Spendiamo qualche riga su questa caratteristica fondamentale della fisica quantistica.
Un modo per figurarci l'entanglement tra due particelle è immaginare di disporre di due monete dotate di una caratteristica particolare: il risultato del lancio di una delle due (Testa o Croce) viene sempre replicato dal lancio dell'altra, ovunque essa si trovi.
Sappiamo dall'esperienza che il lancio di due monete può fornire quattro diversi risultati: TT, TC, CT e CC.
Nel caso specifico di queste monete particolari, se otteniamo T dal lancio della prima sappiamo per certo che otterremo T dal lancio della seconda, indipendentemente dalla distanza a cui le due monete si trovino.
Con “modi statisticamente improbabili” si intende il fatto che, invece di avere (a priori) quattro risultati possibili, ne avremmo solo due: TT oppure CC.
La Meccanica Quantistica rende cioè possibile un nuovo grado di correlazione, più elevato rispetto a quello cui siamo abituati “nel macromondo”: ci informa pure del fatto che, quando due oggetti qualunque interagiscono, generalmente entrano in entanglement e vi rimangono finché restano isolati dal resto del mondo, non importa la misura della distanza con cui vengano in seguito separati.
La distanza non conta! (ecco il principio di non località che inquietava Einsten).
Ryu e Takayanagi intuirono come l’entanglement possa costituire ciò che genera la distanza nello spazio tempo: due regioni di spazio vicine sul lato AdS della dualità - sostenevano - corrispondono a due componenti quantistiche "altamente entangled" della CFT.
Dunque, più grande è l’entanglement tra particelle sulla superficie di confine (lato CFT) più vicine risultano le regioni dello spazio interno (AdS).
.
Se la distanza emerge dall'entaglement non dovremmo più stupirci della caratteristica che aveva turbato Einstein.
Nel 2019 due gruppi di fisici teorici - il primo aveva come portavoce Netta Engelhardt, l’altro Mark Van Raamsdonk - derivano un'idea rivoluzionaria: l'emersione dello spaziotempo sul lato AdS ad opera dell'entanglement quantistico sul lato CFT non riguarda solo il caso dei buchi neri ma l'universo intero.
"... Così come una nube di vapor acqueo con densità ridotta non permette di usare le equazioni dell'idrodinamica - che tuttavia diventano determinanti non appena essa si condensi in una pozza di liquido - nello stesso modo nell'ambito di una CFT con sottosistemi quantistici, ciascuno con campi e particelle senza alcun entanglement, la descrizione AdS equivalente vedrebbe un sistema senza spazio tempo.
Tuttavia non appena l'entanglement dal lato della CFT aumenta, l'entropia di entanglement dei sottosistemi quantistici inizia a corrispondere a frammenti di spaziotempo che emergono nella descrizione AdS.
Inizialmente questi frammenti risultano fisicamente scollegati tra loro - non c'é nessuna possibilità di "spostarsi" da un frammento ad un altro, sono universi diversi privi di connessioni, che tuttavia è possibile descrivere con la Relatività Generale -, ma mano a mano che facciamo aumentare l'entanglement dei sottosistemi quantistici nella CFT, nell'AdS i frammenti dello spaziotempo iniziano a connettersi e ci si ritrova con un volume connesso di spaziotempo.
Ecco che lo spazio tempo si presenta come una rappresentazione geometrica dell'entanglement: nessun entanglement -> niente spaziotempo.
Quindi lo spazio tempo potrebbe consistere in una proprietà emergente di una parte della natura sottostante e ingarbugliata ...
"... se lo spaziotempo emerge dal grado e dalla natura dell'entanglement in un sistema quantistico a bassa dimensione, significa che il sistema quantistico è più 'reale' dello spaziotempo in cui viviamo, così come una cartolina bidimensionale risulta più reale dell'ologramma tridimensionale che crea..."
Riferendoci ad un universo con curvatura AdS, qualora le particelle presenti sulla superficie di confine non siano entangled tra di loro, esso risulta privo di spazio tempo.
Lo spazio tempo compare soltanto quando le particelle sulla superficie esterna diventano entangled: all'aumentare dell'entanglement, diverse regioni di spazio tempo prima disconnesse iniziano a connettersi.
Viceversa, al diminuire dell'entanglement, le regioni connesse si separano diventando disconnesse.
Nello stesso anno altri due gruppi di ricercatori riescono indipendentemente a ricavare la curva di Page avvalendosi di fisica “old style”, e cioè utilizzando soltanto la Relatività Generale e la Meccanica Quantistica (21).
I calcoli da loro svolti dimostrano che la radiazione di Hawking lontana dall’orizzonte e quella interna all’orizzonte sono in realtà due versioni della stessa cosa, confermando così l’idea olografica di cui abbiamo già trattato.
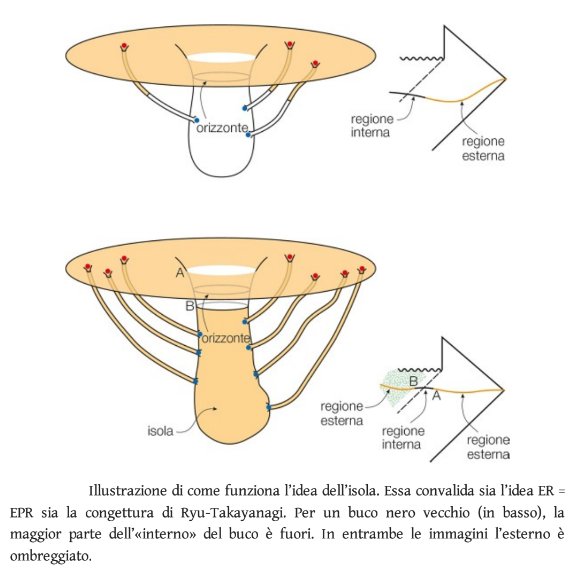
La novità che appare nell’articolo pubblicato è invece la scoperta che un buco nero con un’età maggiore del tempo di Page (quando cioè ha perso oltre la metà della sua massa per effetto della radiazione di Hawking) si trovi nella condizione in cui parte del suo interno sia in realtà già all’esterno dell’orizzonte.
Le implicazioni di questa identità “interno-esterno” sono ancora in parte da comprendere, ma sappiamo che le congetture “RT” ed “ER=EPR” vi svolgono un ruolo importante (22).
Gli autori dell'articolo identificano una regione interna all'orizzonte degli eventi che viene chiamata "isola", la cui ubicazione è determinata dalla quantità di radiazione di Hawking che un osservatore, lontano ma a distanza fissa dal buco nero, sia in grado di raccogliere.
Se il tempo della raccolta è inferiore a quello di Page, l'isola semplicemente non esiste; trascorso il tempo di Page essa compare.
L'isola è delimitata da una superficie sferica chiamata QES (Quantum Extremal Surface), o "Superficie Quantica Estremale".
Risulta, dai calcoli svolti, come l'entropia di entanglement (Sr) sia direttamente proporzionale sia ad una porzione dell'area della QES (area QES/4) che all'entropia di entaglement della radiazione di Hawking (Ssc), quest'ultima ricavata includendo nel calcolo le particelle partner all'interno dell'isola (delle quali il calcolo originale di Hawking non aveva tenuto conto) (21).
Sino a quando almeno la metà della radiazione di Hawking non sia stata emessa, il valore ottenuto dalla nuova formula è identico a quello ottenuto con il conteggio originale (l'entropia cresce sempre): infatti il primo termine dell'addizione è pari a zero (l'isola non esiste ancora).
Trascorso il tempo di Page tuttavia compare l'isola con la sua QES vicina all'orizzonte: le particelle di Hawking presenti all'interno dell'isola risultano "riunite" ai loro partner esterni, e dunque il loro contributo congiunto all'entropia di entanglement si annulla: l'entropia inizia così a diminuire.
Mentre prima del tempo di Page è il secondo termine della somma a determinare l'entropia di entanglement (Ssc), in seguito prevale il primo, e cioè l'area della QES / 4.
Riducendosi l'area dell'orizzonte a causa dell'evaporazione del buco nero, altrettanto fa la QES sino ad annullarsi con la completa scomparsa dell'orizzonte.
Rimane da spiegare come faccia l'informazione ad uscire dal buco nero.
Entrano in gioco le congetture RT e ER=EPR.
La formula relativa all'entropia di entanglement della radiazione di Hawking e quella di Ryu-Takayanagi presentano un alto grado di somiglianza: sembrerebbe esista una connessione tra entanglement e geometria.
La congettura ER=EPR afferma infatti che si possa descrivere l'entanglement tra due particelle qualsiasi - non necessariamente facenti parte della radiazione di Hawking - come se fossero entrambe collegate da un wormhole.
Nel caso di un buco nero, le particelle partner della radiazione di Hawking presenti all'interno sono connesse alla controparte all'esterno dell'orizzonte da minuscoli wormholes.
Considerando l'interno di tali wormholes, diventa difficile definire quale sia lo spazio esterno e quale l'interno di un buco nero: dovremmo riuscire a tracciare nel cunicolo una linea di demarcazione.
Cosa che permette la congettura RT, una volta trovata la superficie di area minima che divide le due regioni.
Quando il buco nero è giovane, l'area minima si ottiene tagliando i wormholes al loro centro.
Quando invece è superato il tempo di Page sono presenti moltissimi wormholes, e sappiamo che la superficie di RT risulta pari alla QES, la "Superficie Quantica Estremale".
Nella figura allegata al post (anche questa ricavata dalla conferenza tenuta da Brian Cox a Genova) vediamo come in quest'ultimo caso l'interno del buco nero sia da considerare al suo esterno.
La singolarità che ne occupava il centro sembra sostituita da una rete quantistica di wormholes che connettono all'esterno.
L'astronauta che attraversa senza alcuna conseguenza l'orizzonte non avrebbe l'incontro con la singolarità distruttiva nel suo futuro, ma si imbatterebbe prima o poi in una rete di wormholes: verrebbe sì disintegrato dalla gravità mareale, ma l'informazione quantistica di cui è composto in un secondo tempo riemergerebbe attraverso questi wormholes, impressa nella radiazione di Hawking.
Rimane ancora un ultimo punto importante di questa lunga digressione: se l'universo così come lo percepiamo è un ologramma con una dimensione in meno codificato su una superficie esterna, ed è l'entanglement a far emergere lo spazio tempo (così come la luce laser fa emergere una terza dimensione spaziale negli ologrammi bidimensionali di uso comune), cosa rende "robusto" lo spazio impedendo che vada in pezzi, ed in che modo?
Dobbiamo cioè trattare del "codice sorgente" dello spazio tempo.
Note:
(19) In realtà il "principio olografico" era già stato formulato a proposito dei buchi neri qualche anno prima da 't Hooft e Susskind.
I due, senza molto successo presso la comunità dei fisici, sostenevano che "le proprietà di una regione dello spazio possano esser completamente codificate dalla sua frontiera", e cioè che la superficie bidimensionale di un buco nero contenga tutte le informazioni necessarie per sapere cosa ci sia al suo interno, che di dimensioni spaziali ne possiede tre.
(20) La congettura Ryu-Takayanagi (RT) del 2006 è una delle idee centrali emerse dall’olografia; la sua validità è già stata dimostrata in parecchi scenari (vedi “Aspects of Holographic Entanglement Entropy”, Journal of High Energy Physics, Ryu S. e Takayanagi T.).
Permette il calcolo della connessione tra entanglement quantistico e geometria dello spaziotempo.
Sfruttando la dualità AdS/CFT stabilisce infatti una connessione tra due numeri:
Il primo numero riguarda un tipo speciale di superficie nel volume dello spazio tempo descritto dalla AdS: la "superficie estremale", cioè il confine intorno al buco nero dove lo spazio tempo passa da una curvatura debole ad una forte.
Il secondo, relativo al sistema quantistico descritto dalla CFT, riguarda "l'entropia di entanglement", la misura cioè di quanto una parte del sistema quantistico sia interconnessa con il resto.
La congettura RT ha dimostrato che l'area della Superficie Estremale di un buco nero nell'AdS è legata all'entropia di entanglement del sistema quantistico nella CFT.
(21) Vedi “The Entropy of Bulk: Quantum Fields and the Entanglement Wedge of an Evaporating Black Hole”, Almheiri A., Engelhardt N., Marolf D. e Maxfield H.
(22): La congettura "ER= EPR" sta per "Einstein Rosenberg = Einstein Podolsky Rosen", un'eguaglianza porposta nel 2013 da Juan Maldacena e Leonard Susskind dove:
ER si riferisce al ponte di Einstein Rosenberg, ciò che oggi è universalmente noto con il termine di "wormhole";
EPR è invece l'analisi condotta da Einstein, Podolsky e Rosen con cui cercarono di farsi una ragione dell'entanglement quantistico.
Secondo gli autori di tale congettura: "... un qualunque sistema correlato secondo EPR deve esser connesso da un qualche genere di ponte ER, anche se questo potrebbe essere un oggetto altamente quantistico ancora da definire ..."
"... congetturiamo che anche il più semplice stato di singoletto di due spin sia connesso da un ponte decisamente quantistico di questo tipo ..."
(23) Ecco la formula calcolata nel 2019 per l'entropia di entanglement:
Sr = (area della QES / 4) + Ssc
dove:
Sr = entropia di entanglement
Ssc = l'entropia di entaglement della radiazione di Hawking che include nel conto le particelle partner all'interno dell'isola







Nessun commento:
Posta un commento